CAPITULO VIII
LA HIPÉRBOLA
Definiciones
Una hipérbola es el lugar geométrico de un punto que se mueve en un plano de tal manera que el valor absoluto de la diferencia de sus distancias a dos puntos fijos del plano, llamados focos, es siempre igual a una cantidad constante, positiva y menor que la distancia entre los focos.
Primera ecuación ordinaria de la hipérbola
Se llama ecuación reducida a la ecuación de la hipérbola cuyos ejes coinciden con los ejes coordenadas, y, por tanto, el centro de hipérbola con el origen de coordenadas.
Si el eje real está en el eje de abscisas las coordenadas de los focos son:
F'(-c,0) y F(c,0)
Cualquier punto de la hipérbola cumple:
Esta expresión da lugar a:
Realizando las operaciones y sabiendo que
b y c" class="i" />, llegamos a:
Asíntotas de la hipérbola
Las asíntotas de la hipérbola (A1 y A2) son las dos líneas rectas que se aproximan cada vez más a la hipérbola pero no llegan a intersectarla. En el infinito las asíntotas estarán a una distancia 0 de ella.
Las ecuaciones de las asíntotas se pueden obtener si se conocen el semieje real (a) y el semieje imaginario (b).

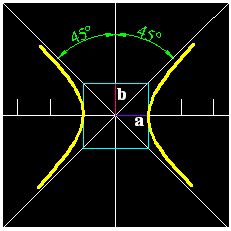
Una hipérbola es equilátera cuando los semiejes a y b son iguales:
Esto quiere decir: a = b.
Si observas las asíntotas, verás que se tratan de las bisectrices (dividen un ángulo en dos partes iguales).
Si observas las asíntotas, verás que se tratan de las bisectrices (dividen un ángulo en dos partes iguales).
Hipérbolas conjugadas
Si dos hipérbolas son tales que ele eje transverso de cada una es idéntico al eje conjugado de la otra, se llaman hipérbolas conjugadas. Cada hipérbola es entonces la hipérbola conjugada de la otra, y también se dice que cada hipérbola es conjugada con respecto a la otra.






No hay comentarios:
Publicar un comentario