CAPITULO IV
ECUACIÓN DE LA CIRCUNFERENCIA
Ecuación de la circunferencia; forma ordinaria
Se obtendrá a partir de la siguiente
DEFINICIÓN. Circunferencia es el lugar geométrico de un punto que se mueve en un plano de tal manera que se conserva siempre a una distancia constante de un punto fijo de ese plano.
El punto fijo se llama centro de la circunferencia, y la distancia constante se llama radio.
Forma general de la ecuación de la circunferencia.
Si desarrollamos la ecuación ordinaria
Se deduce que la ecuación de una circunferencia cualquiera puede escribirse en la forma
llamada forma general de la ecuación de la circunferencia.
Determinación de una circunferencia sujeta a tres condiciones dadas
En la ecuación ordinaria de la circunferencia hay tres constantes arbitrarias independientes, h, k y r. De manera semejante en la ecuación general hay tres constantes arbitrarias independientes, D, E y F.
Como la ecuación de toda circunferencia puede escribirse en cualquiera de las dos formas, la ecuación de cualquier circunferencia particular puede obtenerse determinando los valores de tres constantes.
Esto requiere tres ecuaciones independientes, que pueden obtenerse a partir de tres condiciones independientes. Por tanto, analíticamente, la ecuación de una circunferencia se determina por tres condiciones independientes. Geométricamente, una circunferencia queda perfectamente determinada por tres condiciones independientes; así, por ejemplo, queda determinada por tres cualesquiera de sus puntos.
Familias de circunferencias
Una circunferencia que satisface menos de tres condiciones independientes no es, por lo tanto, única. La ecuación de una circunferencia que satisface solamente a dos condiciones, contiene una constante arbitraria llamada parámetro. Se dice entonces que tal ecuación representa una familia de circunferencias de un parámetro.
Eje radical
El eje radical de dos circunferencias no concéntricas es el lugar geométrico de los puntos con igual potencia respecto de las mismas.
El eje radical es una recta perpendicular al segmento determinado por los dos centros de las circunferencias, pues dado un punto del eje radical, el punto simétrico respecto del segmento que une los centros de las circunferencias también tendrá la misma potencia.
- Si las circunferencias son exteriores, el eje radical se puede determinar uniendo los puntos medios (M en la figura) de los segmentos determinados por los puntos de contacto de las tangentes a las circunferencias (puntos T1 y T2 en la figura).
- Si las circunferencias son tangentes, el eje radical contiene el punto de intersección de ambas circunferencias y es perpendicular a la recta determinada por los centros de las circunferencias.
- Si las circunferencias son secantes, el eje radical contiene los puntos de intersección de las circunferencias, puesto que ambos tienen potencia nula respecto de las circunferencias.
- Si una de las circunferencias es interior, se puede obtener el eje radical trazando una circunferencia auxiliar secante a las circunferencias dadas (a en la figura). El punto de intersección de los ejes radicales auxiliares (C en la figura) tiene igual potencia respecto a las circunferencias dadas, por tanto, el eje radical será la recta que contiene al punto C y es perpendicular a la recta determinada por los centros de las circunferencias iniciales. (Se debe elegir la circunferencia auxiliar de tal forma que los ejes radicales auxiliares se corten dentro del papel del dibujo).
Tangente a una curva
Una recta tangente a una curva en un punto de ella, es una recta que al pasar por dicho punto tiene la misma pendiente de la curva. La recta tangente es un caso particular de espacio tangente a una variedad diferenciable de dimensión 1, \R^1.
DEFINICIÓN.
Sea  una curva, y
una curva, y  un punto regular de esta, es decir, un punto no anguloso donde la curva es diferenciable, y por tanto en
un punto regular de esta, es decir, un punto no anguloso donde la curva es diferenciable, y por tanto en  la curva no cambia repentinamente de dirección. La tangente a
la curva no cambia repentinamente de dirección. La tangente a  en
en  es la recta
es la recta  que pasa por
que pasa por  y que tiene la misma dirección que
y que tiene la misma dirección que  alrededor de
alrededor de  .
.
 una curva, y
una curva, y  un punto regular de esta, es decir, un punto no anguloso donde la curva es diferenciable, y por tanto en
un punto regular de esta, es decir, un punto no anguloso donde la curva es diferenciable, y por tanto en  la curva no cambia repentinamente de dirección. La tangente a
la curva no cambia repentinamente de dirección. La tangente a  en
en  es la recta
es la recta  que pasa por
que pasa por  y que tiene la misma dirección que
y que tiene la misma dirección que  alrededor de
alrededor de  .
.
La tangente es la posición límite de la recta secante ( ) (el segmento
) (el segmento  se llama cuerda de la curva), cuando
se llama cuerda de la curva), cuando 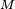 es un punto de
es un punto de  que se aproxima indefinidamente al punto
que se aproxima indefinidamente al punto  (
(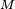 se desplaza sucesivamente por
se desplaza sucesivamente por 
 ) (el segmento
) (el segmento  se llama cuerda de la curva), cuando
se llama cuerda de la curva), cuando 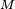 es un punto de
es un punto de  que se aproxima indefinidamente al punto
que se aproxima indefinidamente al punto  (
(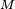 se desplaza sucesivamente por
se desplaza sucesivamente por 
Si  es punto de una función f (no es el caso en el gráfico precedente), entonces la recta
es punto de una función f (no es el caso en el gráfico precedente), entonces la recta  tendrá como coeficiente director (opendiente):
tendrá como coeficiente director (opendiente):
 es punto de una función f (no es el caso en el gráfico precedente), entonces la recta
es punto de una función f (no es el caso en el gráfico precedente), entonces la recta  tendrá como coeficiente director (opendiente):
tendrá como coeficiente director (opendiente):
Donde  son las coordenadas del punto
son las coordenadas del punto  y
y  las del punto
las del punto 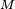 . Por lo tanto, la pendiente de la tangente TAserá:
. Por lo tanto, la pendiente de la tangente TAserá:
 son las coordenadas del punto
son las coordenadas del punto  y
y  las del punto
las del punto 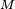 . Por lo tanto, la pendiente de la tangente TAserá:
. Por lo tanto, la pendiente de la tangente TAserá:
Es, por definición, f '(a), la derivada de f en a.
La ecuación de la tangente es  :
:
 :
:
La recta ortogonal a la tangente  que pasa por el punto
que pasa por el punto  se denomina recta normal y su pendiente, en un sistema de coordenadas ortonormales, es dada por
se denomina recta normal y su pendiente, en un sistema de coordenadas ortonormales, es dada por 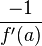 . Siendo su ecuación:
. Siendo su ecuación:
 que pasa por el punto
que pasa por el punto  se denomina recta normal y su pendiente, en un sistema de coordenadas ortonormales, es dada por
se denomina recta normal y su pendiente, en un sistema de coordenadas ortonormales, es dada por 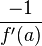 . Siendo su ecuación:
. Siendo su ecuación:
suponiendo claro está que  . Si
. Si  entonces la recta normal es simplemente
entonces la recta normal es simplemente  .
.
 . Si
. Si  entonces la recta normal es simplemente
entonces la recta normal es simplemente  .
.



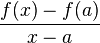



No hay comentarios:
Publicar un comentario