CAPITULO IX
ECUACIÓN GENERAL DE SEGUNDO GRADO
Transformación de la ecuación general por rotación de los ejes coordenados
Definición general de cónica
Se denomina sección cónica (o simplemente cónica) a todas las curvas intersección entre un cono y un plano; si dicho plano no pasa por el vértice, se obtienen las cónicas propiamente dichas. Se clasifican en tres tipos: elipse, parábola e hipérbola. un cono circular recto de dos hojas con un plano que no pasa por su vértice
De acuerdo al ángulo y el lugar de la intersección es posible obtener círculos, hipérbolas , elipses o parábolas. Cuando el plano solo toca uno de los mantos del cono y no es paralelo a una de sus aristas se obtiene una Elipse. Cuando el plano corta los dos mantos del cono se obtiene una hipérbola. Cuando el plano que corta es paralelo a una de las aristas del cono se obtiene una parábola.
 Tipos:
Tipos:
En función de la relación existente entre el ángulo de conicidad (α) y la inclinación del plano respecto del eje del cono (β), pueden obtenerse diferentes secciones cónicas, a saber:

Si el plano pasa por el vértice del cono, se puede comprobar que:
Cuando β > α la intersección es un único punto (el vértice).
Cuando β = α la intersección es una recta generatriz del cono (el plano será tangente al cono).
Cuando β < α la intersección vendrá dada por dos rectas que se cortan en el vértice.
cuando β = 90º El ángulo formado por las rectas irá aumentando a medida β disminuye, hasta alcanzar el máximo (α) cuando el plano contenga al eje del cono (β = 0).
Transformación de la ecuación general por rotación de los ejes coordenados
Definición general de cónica
Se denomina sección cónica (o simplemente cónica) a todas las curvas intersección entre un cono y un plano; si dicho plano no pasa por el vértice, se obtienen las cónicas propiamente dichas. Se clasifican en tres tipos: elipse, parábola e hipérbola. un cono circular recto de dos hojas con un plano que no pasa por su vértice
De acuerdo al ángulo y el lugar de la intersección es posible obtener círculos, hipérbolas , elipses o parábolas. Cuando el plano solo toca uno de los mantos del cono y no es paralelo a una de sus aristas se obtiene una Elipse. Cuando el plano corta los dos mantos del cono se obtiene una hipérbola. Cuando el plano que corta es paralelo a una de las aristas del cono se obtiene una parábola.
 Tipos:
Tipos:En función de la relación existente entre el ángulo de conicidad (α) y la inclinación del plano respecto del eje del cono (β), pueden obtenerse diferentes secciones cónicas, a saber:
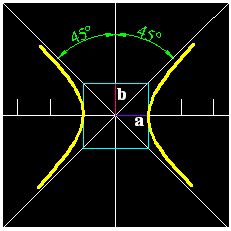
- β < α : Hipérbola (naranja)
- β = α : Parábola (azulado)
- β > α : Elipse (verde)
- β = 90º: Circunferencia (un caso particular de elipse) (rojo)

Si el plano pasa por el vértice del cono, se puede comprobar que:
Cuando β > α la intersección es un único punto (el vértice).
Cuando β = α la intersección es una recta generatriz del cono (el plano será tangente al cono).
Cuando β < α la intersección vendrá dada por dos rectas que se cortan en el vértice.
cuando β = 90º El ángulo formado por las rectas irá aumentando a medida β disminuye, hasta alcanzar el máximo (α) cuando el plano contenga al eje del cono (β = 0).
Sistema de cónicas
La perspectiva cónica es un sistema de representación gráfico basado en la proyección de un cuerpo tridimensional sobre un plano auxiliándose en rectas proyectantes que pasan por un punto. El resultado se aproxima a la visión obtenida si el ojo estuviera situado en dicho punto.
Filippo Brunelleschi en el Quattrocento fue el primero que formuló las leyes de la perspectiva cónica, mostrando en sus dibujos las construcciones en planta y alzado, indicando las líneas que se dirigen al punto de fuga.
Una familia de cónicas interesante es el sistema formado por las cónicas que pasan por las intersecciones de dos cónicas dadas.



























 ) (el segmento
) (el segmento 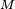 es un punto de
es un punto de 
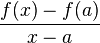
 son las coordenadas del punto
son las coordenadas del punto  las del punto
las del punto 

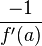 . Siendo su ecuación:
. Siendo su ecuación:
 . Si
. Si  entonces la recta normal es simplemente
entonces la recta normal es simplemente  .
.